Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 6√3r.
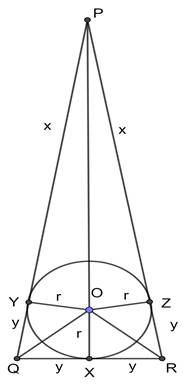
Let PQR is the triangle with inscribed circle of radius ‘r’, touching sides PQ at Y, QR at X and PR at Z.
OZ, OX, OY are perpendicular to the sides PR,QR,PQ.
Here PQR is an isosceles triangle with sides PQ = PR and also from the figure,
⇒ PY = PZ = x
⇒ YQ = QX = XR = RZ = y
From the figure we can see that,
⇒ Area(ΔPQR) = Area(ΔPOR) + Area(ΔPOQ) + Area(ΔQOR)
We know that area of a triangle = ![]() ×base×height
×base×height
⇒ ![]()
⇒ 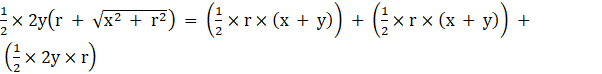
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]() …… (1)
…… (1)
We know that perimeter of the triangle is Per = PQ + QR + RP
⇒ PER = (x + y) + (x + y) + 2y
⇒ PER = 2x + 4y …… (2)
From(1)
⇒ ![]()
⇒ ![]()
⇒ ![]()
We need perimeter to be minimum and let us PER as the function of y,
We know that for maxima and minima ![]() ,
,
⇒ 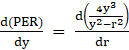
⇒ 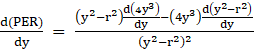
⇒ ![]()
⇒ ![]()
⇒ 4y4 - 12y2r2 = 0
⇒ 4y2(y2 - 3r2) = 0
⇒ ![]()
Differentiating PER again,
⇒ ![]()
⇒ 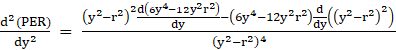
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]()
⇒ ![]() >0(minima)
>0(minima)
We got minima at y = ![]() r.
r.
Let’s find the value of x,
⇒ ![]()
⇒ x = ![]() r
r
⇒ PER = 2(![]() r) + 4(
r) + 4(![]() r)
r)
⇒ PER = 6![]() r
r
∴ Thus proved