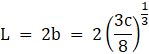A box of constant volume c is to be twice as long as it is wide. The material on the top and four sides cost three times as much per square metre as that in the bottom. What are the most economic dimensions?
Let,
Width = b
Length L = 2b
Height = h
Cost of material on top and 4 sides = 3 x cost of material at bottom.
Here we do not have individual cost per area of different materials. But we can use the total surface area of individual parts as replacement for the cost.
bx2b + 2(hxb) + 2(hx2b) = 3(bx2b)
2b2 + 2hb + 4hb = 6b2
6hb = 4b2
![]()
Volume of the box = c = bx2bxh = 2b2h
Therefore,
![]()
We want the optimum dimensions of the box. We find this by optimizing the total surface area to be minimum. This is because the majority of the surface costs more.
Surface area(total) = S = 2(bh + 2bh + 2b2) = 2(2b2 + 3bh)
![]()
![]()
![]()
![]()
![]()
A minima exists at 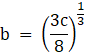
Therefore:
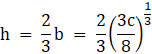
And Length = 2b