A wholesale dealer deals in two kinds, A and B (say) of mixture of nuts. Each kg of mixture A contains 60 grams of almonds, 30 grams of cashew nuts and 30 grams of hazel nuts. Each kg of mixture B contains 30 grams of almonds, 60 grams of cashew nuts and 180 grams of hazel nuts. The remainder of both mixtures is per nuts. The dealer is contemplating to use of cashew nuts and 540 grams of hazel nuts. Mixture A costs ₹ 8 per kg. and mixture B costs ₹ 12 per kg. Assuming that mixtures A and B are uniform, use graphical method to determine the number of kg. of each mixture he should use to minimize the cost of the bag.
The above information can be expressed in the form of the following table:
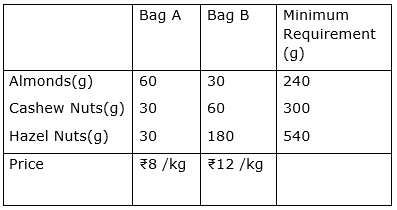
Let the number of bags chosen of A and B be ‘x’ and ‘y’ respectively.
Cost of Bag A = 8x
Cost of Bag B = 12y
Total Cost of Bags = 8x + 12 y
Now,
⟹ 60x + 30y ≥ 240
i.e. the minimum requirement of almonds from both the bags is 240g, each of which contains 60g and 30g of almonds respectively.
⟹ 30x + 60y ≥ 300
i.e. the minimum requirement of Cashew Nuts from both the bags is 300g, each of which contains 30g and 60g of cashew nuts respectively.
⟹ 30x + 180y ≥ 540
i.e. the minimum requirement of Hazel Nuts from both the bags is 540g, each of which contains 30g and 180g of hazelnut respectively.
Hence, mathematical formulation of the LPP is as follows:
Find ‘x’ and ‘y’ that
Minimises Z = 8x + 12y
Subject to the following constraints:
(i) 60x + 30y ≥ 240
i.e. 2x + y ≥ 8
(ii) 30x + 60y ≥ 300
i.e. x + 2y ≥ 10
(iii) 30x + 180y ≥ 540
i.e. x + 6y ≥ 18
(iv) x,y ≥ 0 (∵ quantity cant be negative)
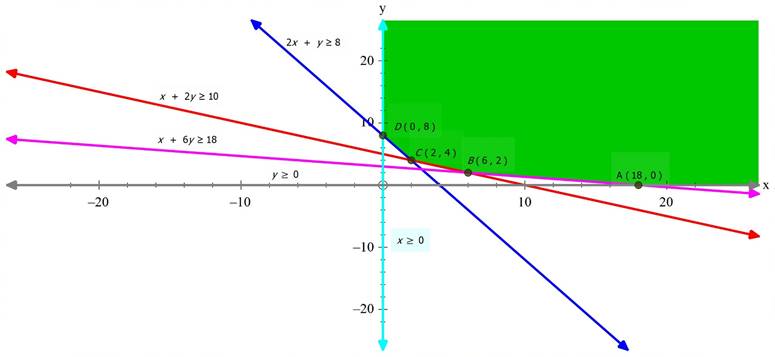
The feasible region is unbounded.
The corner points of the feasible region are as follows:
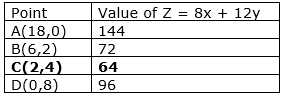
Z is smallest at C(2,4)
Let us consider 8x + 12y ≤ 64
As this has no intersection with the feasible region, the smallest value is the minimum value.
The minimum cost of the bags is ₹64