As we need to find

We can directly find the limiting value of a function by putting the value of the variable at which the limiting value is asked if it does not take any indeterminate form (0/0 or ∞/∞ or ∞-∞,1^∞ .. etc.)

Let Z =

As it is taking indeterminate form-

∴ we need to take steps to remove this form so that we can get a finite value.

As, Z =

⇒ Z =

Taking log both sides-

⇒ log Z =

⇒ log Z =

{∵ log a^m = m log a}

Now it gives us a form that can be reduced to

log Z =

{adding and subtracting 1 to cos x to get the form}

Dividing numerator and denominator by cos x + sin x– 1 to match with form in formula

∴ log Z =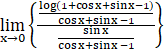

using algebra of limits –

log Z =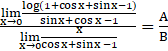

∴ A =

Let, cos x + sin x - 1 = y

As x→0 ⇒ y→0

∴ A =

Use the formula -

∴ A = 1

Now, B =

∵ cos x – 1 = -2sin²(x/2) and sin x = 2sin(x/2)cos(x/2)

⇒ B =

⇒ B =

⇒ B =

Use the formula -

⇒ B =

∴ B = 1

Hence,

log Z =

⇒ log_e Z = 1

∴ Z = e¹ = e

Hence,