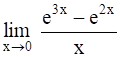
As we need to find

We can directly find the limiting value of a function by putting the value of the variable at which the limiting value is asked if it does not take any indeterminate form (0/0 or ∞/∞ or ∞-∞, .. etc.)

Let Z =

∴ we need to take steps to remove this form so that we can get a finite value.

TIP: Most of the problems of logarithmic and exponential limits are solved using the formula and

This question is a direct application of limits formula of exponential and logarithmic limits.

As Z =

⇒ Z =

{Adding and subtracting 1 in numerator}

⇒ Z =

{using algebra of limits}

To get the form as present in the formula we multiply and divide 3 and 2 into both terms respectively:

⇒ Z =

Use the formula:

∴ Z = 3log e – 2log e= 3-2 = 1

{using log e = 1}

Hence,