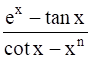
Let, y =

We have to find dy/dx

As we can observe that y is a fraction of two functions say u and v where,

u = e^x – tan x and v = cot x – xⁿ

∴ y = u/v

As we know that to find the derivative of fraction of two function we apply quotient rule of differentiation.

By quotient rule, we have –

…equation 1

As, u = e^x – tan x

∴

∵ , so we get –

⇒ …equation 2

As, v = cot x – xⁿ

∵ , so we get –

⇒ …equation 3

∴ from equation 1, we can find dy/dx

∴

using equation 2 and 3, we get –

⇒

⇒

Hence,