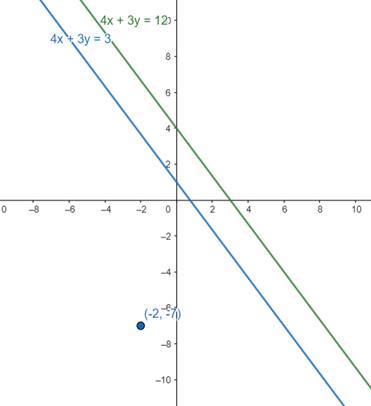
Find the equation of straight line passing through ( – 2, – 7) and having an intercept of length 3 between the straight lines 4x + 3y = 12 and 4x + 3y = 3.
Given: (x1,y1) = A ( – 2, – 7)
To find:
Equation of required line.
Explanation:
So, the equation of the line is
Formula Used: ![]()
![]()
Let the required line intersect the lines 4x + 3y = 3 and 4x + 3y = 12 at P1 and P2.
Let AP1 = r1 and AP2 = r2
Then, the coordinates of P1 and P2 are given by ![]() and
and ![]() respectively. Thus, the coordinates of P1 and P2 are ( – 2 + r1cos θ, – 7 + r1sin θ) and ( – 2 + r2cos θ, – 7 + r2sin θ), respectively.
respectively. Thus, the coordinates of P1 and P2 are ( – 2 + r1cos θ, – 7 + r1sin θ) and ( – 2 + r2cos θ, – 7 + r2sin θ), respectively.
Clearly, the points P1 and P2 lie on the lines 4x + 3y = 3 and 4x + 3y = 12
4( – 2 + r1cos θ) + 3( – 7 + r1sin θ) = 3 and 4( – 2 + r2cos θ) + 3( – 7 + r2sin θ) = 12,
![]() and
and ![]()
Here AP2 – AP1 = 3
![]()
![]()
⇒ 3 = 4 cos θ + 3 sin θ
⇒ 3(1 – sin θ) = 4cos θ
⇒ 9(1 + sin2 θ – 2sin θ) = 16 cos2 θ = 16(1 – sin2 θ)
⇒ 25 sin2 θ – 18 sin θ – 7 = 0
⇒ (sin θ – 1)(25 sin θ + 7 ) = 0
⇒ Sin θ = 1, sin θ = – 7/25
⇒ Cos θ = 0, cos θ = 24/25
Thus, the equation of the required line is
x + 2 = 0 or ![]()
⇒ x + 2 = 0 or 7x + 24 y + 182 = 0
Hence, the equation of line is x + 2 = 0 or 7x + 24 y + 182 = 0