If the straight line 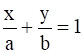 passes through the point of intersection of the lines x + y = 3 and 2x – 3y = 1 and is parallel to x – y – 6 = 0, find a and b.
passes through the point of intersection of the lines x + y = 3 and 2x – 3y = 1 and is parallel to x – y – 6 = 0, find a and b.
Given: lines are x + y = 3 and 2x − 3y = 1.
To find:
a and b.
Concept Used:
Point of intersection of two lines.
Explanation:
x + y − 3 = 0 … (1)
2x − 3y − 1 = 0 … (2)
Solving (1) and (2) using cross - multiplication method:
![]()
⇒ x = 2 , y = 1
Thus, the point of intersection of the given lines is (2, 1).
It is given that the line ![]() passes through (2, 1).
passes through (2, 1).
∴ ![]() ……(3)
……(3)
It is also given that the line ![]() is parallel to the line x − y − 6 = 0.
is parallel to the line x − y − 6 = 0.
Hence, Slope of ![]() is equal to the slope of x − y − 6 = 0 or, y = x – 6
is equal to the slope of x − y − 6 = 0 or, y = x – 6
∴ - b/a = 1
⇒ b = - a … (4)
From (3) and (4):
∴ ![]()
⇒ a = 1
From (4):
b = −1
∴ a = 1,
b = −1
Hence, a = 1, b = - 1
10