Prove that the points (2, -1), (0, 2), (2, 3) and (4, 0) are the coordinates of the vertices of a parallelogram and find the angle between its diagonals.
To prove:
The points (2, -1), (0, 2), (2, 3) and (4, 0) are the coordinates of the vertices of a parallelogram
To find:
The angle between diagonals of parallelogram.
Assuming:
A(2, − 1), B(0, 2), C(2, 3) and D(4, 0) be the vertices.
Explanation:
Slope of AB ![]()
Slope of BC ![]()
Slope of CD![]()
Slope of DA ![]()
Thus, AB is parallel to CD and BC is parallel to DA.
Therefore, the given points are the vertices of a parallelogram.
Now, let us find the angle between the diagonals AC and BD.
Let m1 and m2 be the slopes of AC and BD, respectively.
∴ ![]()
∴ ![]()
Thus, the diagonal AC is parallel to the y-axis.
∴∠ODB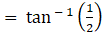
In triangle MND,
∠DMN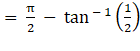
Hence proved, the acute angle between the diagonal is 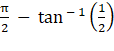 .
.