Given:

x + 2y + 3 = 0 and 3x + 4y + 7 = 0

To find:

The equation of a straight line passing through the point of intersection of x + 2y + 3 = 0 and 3x + 4y + 7 = 0 and perpendicular to the straight line x – y + 9 = 0.

Explanation:

The equation of the straight line passing through the points of intersection of x + 2y + 3 = 0 and 3x + 4y + 7 = 0 is

x + 2y + 3 + λ(3x + 4y + 7) = 0

⇒ (1 + 3λ)x + (2 + 4λ)y + 3 + 7λ = 0

⇒ y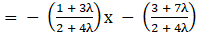

The required line is perpendicular to x − y + 9 = 0 or, y = x + 9

∴

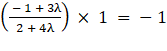
⇒ λ = -1

Required equation is given below:

(1 − 3)x + (2 − 4)y + 3 − 7 = 0

⇒ x + y + 2 = 0

Hence, required equation is x + y + 2 = 0