Given:

Lines represented by x(1 + λ) + y(2 – λ) + 5 = 0, λ being arbitrary

To prove:

The family of lines represented by x(1 + λ) + y(2 – λ) + 5 = 0, λ being arbitrary, pass through a fixed point. Also, find the fixed point.

Explanation:

The given family of lines can be written as

x + 2y + 5 + λ (x − y) = 0

This line is of the form L₁ + λL₂ = 0, which passes through the intersection of L₁ = 0 and L₂ = 0.
⇒ x + 2y + 5 = 0
⇒ x − y = 0

Now, solving the lines: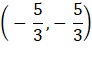
This is a fixed point.

Hence proved.