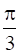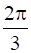Find the lines through the point (0, 2) making angles and with the x–axis. Also, find the lines parallel to them cutting the y–axis at a distance of 2 units below the origin.

Question

Philoid · Accepted Answer

We know that equation of line having angle θ from x–axis and passing through (x₁, y₁) is given by,

Therefore,

Equation of first line,

(y – 2)

y – 2 = √3x

y – √3x – 2 = 0

The equation of line parallel to this line and passing through (0, –2),

(y + 2) = √3x

y – √3x + 2 = 0

Equation of second line,

(y – 2)

y – 2 = –√3x

y + √3x – 2 = 0

The equation of line parallel to this line and passing through (0, –2),

(y + 2) = –√3x

y + √3x + 2 = 0