In the matrix 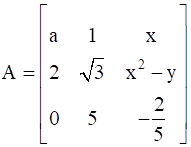 , write:
, write:
(i) The order of the matrix A
(ii) The number of elements
(iii) Write elements a23, a31, a12
We have the matrix

A matrix, as we know, is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns.
(i). We need to find the order of the matrix A.
And we know that,
The number of rows and columns that a matrix has is called its order or its dimension. By convention, rows are listed first; and columns second.
So,
Here, in matrix A:
There are 3 rows.
Elements in 1st row = a, 1, x
Elements in 2nd row = 2, √3, x2 – y
Elements in 3rd row = 0, 5, -2/5
⇒ M = 3
And,
There are 3 columns.
Elements in 1st column = a, 2, 0
Elements in 2nd column = 1, √3, 5
Elements in 3rd column = x, x2 – y, -2/5
⇒ N = 3
Since, the order of matrix = M × N
⇒ The order of matrix A = 3 × 3
Thus, the order of the matrix A is 3 × 3.
(ii). We need to find the number of elements in the matrix A.
And we know that,
Each number that makes up a matrix is called an element of the matrix.
So,
If a matrix has M rows and N columns, the number of elements is MN.
Here, in matrix A:
There are 3 rows.
⇒ M = 3
And,
There are 3 columns.
⇒ N = 3
Then, number of elements = MN
⇒ Number of elements = 3 × 3
⇒ Number of elements = 9
The elements are namely, a, 2, 0, 1, √3, 5, x, x2 – y, -2/5.
Thus, the number of elements is 9.
(iii). We need to find the elements a23, a31 and a12.
We know that,
aij is the representation of elements lying in the ith row and jth column.
For a23:
Comparing aij with a23, we have
i = 2
j = 3
Look up in matrix A for element in (i=) 2nd row and (j=) 3rd column.

Element that is common to both 2nd row and 3rd column = x2 – y
⇒ a23 = x2 – y
For a31:
Comparing aij with a31, we have
i = 3
j = 1
Look up in matrix A for element in (i=) 3rd row and (j=) 1st column.

Element that is common to both 3rd row and 1st column = 0
⇒ a31 = 0
For a12:
Comparing aij with a12, we have
i = 1
j = 2
Look up in matrix A for element in (i=) 1st row and (j=) 2nd column.

Element that is common to both 1st row and 2nd column = 1
⇒ a12 = 1
Thus, a23 = x2 – y, a31 = 0 and a12 = 1.