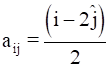We know that,

A matrix, as we know, is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns.

Also,

We know that, the notation A = [a_ij]_m×m indicates that A is a matrix of order m × n, also 1 ≤ i ≤ m, 1 ≤ j ≤ n; i, j ∈ N.

(i).We need to construct a matrix, a_2×2, where

For a_2×2,

1 ≤ i ≤ m

⇒ 1 ≤ i ≤ 2 [∵ m = 2]

And,

1 ≤ j ≤ n

⇒ 1 ≤ j ≤ 2 [∵ n = 2]

Put i = 1 and j = 1.

Put i = 1 and j = 2.

Put i = 2 and j = 1.

⇒ a₂₁ = 0

Put i = 2 and j = 2.

⇒ a₂₂ = 2

Let the matrix formed be A.

Substituting the values of a₁₁, a₁₂, a₂₁ and a₂₂, we get the matrix

(ii). We need to construct a matrix, a_2×2, where

a_ij = |-2i + 3j|

For a_2×2,

1 ≤ i ≤ m

⇒ 1 ≤ i ≤ 2 [∵ m = 2]

And,

1 ≤ j ≤ n

⇒ 1 ≤ j ≤ 2 [∵ n = 2]

Put i = 1 and j = 1.

a₁₁ = |-2(1) + 3(1)|

⇒ a₁₁ = |-2 + 3|

⇒ a₁₁ = |1|

⇒ a₁₁ = 1

Put i = 1 and j = 2.

a₁₂ = |-2(1) + 3(2)|

⇒ a₁₂ = |-2 + 6|

⇒ a₁₂ = |4|

⇒ a₁₂ = 4

Put i = 2 and j = 1.

a₂₁ = |-2(2) + 3(1)|

⇒ a₂₁ = |-4 + 3|

⇒ a₂₁ = |-1|

⇒ a₂₁ = 1

Put i = 2 and j = 2.

a₂₂ = |-2(2) + 3(2)|

⇒ a₂₂ = |-4 + 6|

⇒ a₂₂ = |2|

⇒ a₂₂ = 2

Let the matrix formed be A.

Substituting the values of a₁₁, a₁₂, a₂₁ and a₂₂, we get the matrix