Find values of a and b if A = B, where
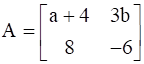 and
and 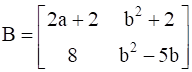
We have the matrices A and B, where
![]()
![]()
We need to find the values of a and b.
We know that, if
![]()
Then,
a11 = b11
a12 = b12
a21 = b21
a22 = b22
Also, A = B.
![]()
This means,
a + 4 = 2a + 2 …(i)
3b = b2 + 2 …(ii)
8 = 8
-6 = b2 – 5b …(iii)
From equation (i), we can find the value of a.
a + 4 = 2a + 2
⇒ 2a – a = 4 – 2
⇒ a = 2
From equation (ii), we can find the value of b2.
3b = b2 + 2
⇒ b2= 3b – 2
Substitute the value of b2 in equation (iii), we get
-6 = b2 – 5b
⇒ -6 = (3b – 2) – 5b
⇒ -6 = 3b – 2 – 5b
⇒ -6 = 3b – 5b – 2
⇒ -6 = -2b – 2
⇒ 2b = 6 – 2
⇒ 2b = 4
![]()
⇒ b = 2
Thus, a = 2 and b = 2.
7