If possible, find the sum of the matrices A and B, where 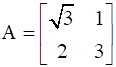 and
and 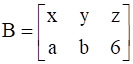 .
.
We know that,
The number of rows and columns that a matrix has is called its order or its dimension. By convention, rows are listed first; and columns second.
Also,
Addition or subtraction of matrices is possible only if the matrices are of same order.
That is,
If A and B are two matrices and if they are needed to be added, then if order of A is m × n, order of B must be m × n.
We have matrices A and B, where
![]()
![]()
We know what order of matrix is,
If a matrix has M rows and N columns, the order of matrix is M × N.
In matrix A:
Number of rows = 2
⇒ M = 2
Number of column = 2
⇒ N = 2
Then, order of matrix A = M × N
⇒ Order of matrix A = 2 × 2
In matrix B:
Number of rows = 2
⇒ M = 2
Number of columns = 3
⇒ M = 3
Then, order of matrix B = M × N
⇒ order of matrix B = 2 × 3
Since,
Order of matrix A ≠ Order of matrix B
⇒ Matrices A and B cannot be added.
Thus, matrix A and matrix B cannot be added.