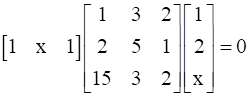
We have the matrix equation,

We need to find the value of x.

Let us compute L.H.S:

Let,

and

In order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.

First, let us compute

Multiply 1^st row of matrix A by matching members of 1^st column of matrix B, then sum them up.

(1, x, 1).(1, 2, 15) = (1 × 1) + (x × 2) + (1 × 15)

⇒ (1, x, 1).(1, 2, 15) = 1 + 2x + 15

⇒ (1, x, 1).(1, 2, 15) = 2x + 16

Multiply 1^st row of matrix A by matching members of 2^nd column of matrix B, then sum them up.

(1, x, 1).(3, 5, 3) = (1 × 3) + (x × 5) + (1 × 3)

⇒ (1, x, 1).(3, 5, 3) = 3 + 5x + 3

⇒ (1, x, 1).(3, 5, 3) = 5x + 6

Multiply 1^st row of matrix A by matching members of 3^rd column of matrix B, then sum them up.

(1, x, 1).(2, 1, 2) = (1 × 2) + (x × 1) + (1 × 2)

⇒ (1, x, 1).(2, 1, 2) = 2 + x + 2

⇒ (1, x, 1).(2, 1, 2) = x + 4

So,

Now, compute

Multiply 1^st row of matrix D by matching members of 1^st column of matrix C, then sum them up.

(2x + 16, 5x + 6, x + 4).(1, 2, x) = ((2x + 16) × 1) + ((5x + 6) × 2) + ((x + 4) × x)

⇒ (2x + 16, 5x + 6, x + 4).(1, 2, x) = (2x + 16) + (10x + 12) + (x² + 4x)

⇒ (2x + 16, 5x + 6, x + 4).(1, 2, x) = x² + 2x + 10x + 4x + 16 + 12

⇒ (2x + 16, 5x + 6, x + 4).(1, 2, x) = x² + 16x + 28

So, we have got

Now, put L.H.S = R.H.S

[x² + 16x + 28] = [0]

This means,

x² + 16x + 28 = 0

⇒ x² + 14x + 2x + 28 = 0

⇒ x(x + 14) + 2(x + 14) = 0

⇒ (x + 2)(x + 14) = 0

⇒ (x + 2) = 0 or (x + 14) = 0

⇒ x = -2 or x = -14

Thus, x = -2, -14.