Show that 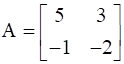 satisfies the equation A2 – 3A – 7I = 0 and hence find A–1.
satisfies the equation A2 – 3A – 7I = 0 and hence find A–1.
We have the matrix A, such that
![]()
(i). We need to show that the matrix A satisfies the equation A2 – 3A – 7I = 0.
(ii). Also, we need to find A-1.
(i). Take L.H.S: A2 – 3A – 7I
First, compute A2.
A2 = A.A
![]()
In order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.
Multiply 1st row of matrix A by matching members of 1st column of matrix A, then sum them up.
(5, 3).(5, -1) = (5 × 5) + (3 × -1)
⇒ (5, 3).(5, -1) = 25 + (-3)
⇒ (5, 3).(5, -1) = 25 – 3
⇒ (5, 3).(5, -1) = 22
![]()
Multiply 1st row of matrix A by matching members of 2nd column of matrix A, then sum them up.
(5, 3).(3, -2) = (5 × 3) + (3 × -2)
⇒ (5, 3).(3, -2) = 15 + (-6)
⇒ (5, 3).(3, -2) = 15 – 6
⇒ (5, 3).(3, -2) = 9
![]()
Multiply 2nd row of matrix A by matching members of 1st column of matrix A, then sum them up.
(-1, -2).(5, -1) = (-1 × 5) + (-2 × -1)
⇒ (-1, -2).(5, -1) = -5 + 2
⇒ (-1, -2).(5, -1) = -3
![]()
Multiply 2nd row of matrix A by matching members of 2nd column of matrix A, then sum them up.
(-1, -2).(3, -2) = (-1 × 3) + (-2 × -2)
⇒ (-1, -2).(3, -2) = -3 + 4
⇒ (-1, -2).(3, -2) = 1
![]()
![]()
Substitute values of A2 and A in A2 – 3A – 7I.
![]()
Also, since matrix A is of the order 2 × 2, then I will be the identity matrix of order 2 × 2 such that,
![]()
![]()
![]()
![]()
![]()
![]()
Clearly,
L.H.S = R.H.S
Thus, we have shown that matrix A satisfy A2 – 3A – 7I = 0.
(ii). Now, let us find A-1.
We know that, inverse of matrix A is A-1 is true only when
A × A-1 = A-1 × A = I
Where, I = Identity matrix
We have,
A2 – 3A – 7I = 0
Multiply A-1 on both sides, we get
A-1(A2 – 3A – 7I) = A-1 × 0
⇒ A-1.A2 – A-1.3A – A-1.7I = 0
⇒ A-1.A.A – 3A-1.A – 7A-1.I = 0
⇒ (A-1A)A – 3(A-1A) – 7(A-1I) = 0
And as A-1A = I and A-1I = A-1
⇒ IA – 3I – 7A-1 = 0
Since, IA = A
⇒ A – 3I – 7A-1 = 0
⇒ 7A-1 = A – 3I
![]()
![]() [∵
[∵ ![]() ]
]
![]()
![]()
![]()
Thus, ![]() .
.