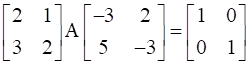
Here we have been given a matrix equation,

We need to find the matrix A.

Let matrix A be of order 2 × 2, and can be represented as

Then, we get

Take L.H.S:

So, first let us calculate

In order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.

Multiply 1^st row of matrix X by matching members of 1^st column of matrix Y, then sum them up.

(2, 1).(a, c) = (2 × a) + (1 × c)

⇒ (2, 1).(a, c) = 2a + c

Multiply 1^st row of matrix X by matching members of 2^nd column of matrix Y, then sum them up.

(2, 1).(b, d) = (2 × b) + (1 × d)

⇒ (2, 1).(b, d) = 2b + d

Multiply 2^nd row of matrix X by matching members of 1^st column of matrix Y, then sum them up.

(3, 2).(a, c) = (3 × a) + (2 × c)

⇒ (3, 2).(a, c) = 3a + 2c

Multiply 2^nd row of matrix X by matching members of 2^nd column of matrix Y, then sum them up.

(3, 2).(b, d) = (3 × b) + (2 × d)

⇒ (3, 2).(b, d) = 3b + 2d

Let X.Y = Z

Now, we need to find .

That is,

Where, let .

Multiply 1^st row of matrix Z by matching members of 1^st column of matrix Q, then sum them up.

(2a + c, 2b + d).(-3, 5) = ((2a + c) × -3) + ((2b + d) × 5)

⇒ (2a + c, 2b + d).(-3, 5) = -6a – 3c + 10b + 5d

⇒ (2a + c, 2b + d).(-3, 5) = -6a + 10b – 3c + 5d

Multiply 1^st row of matrix Z by matching members of 2^nd column of matrix Q, then sum them up.

(2a + c, 2b + d).(2, -3) = ((2a + c) × 2) + ((2b + d) × -3)

⇒ (2a + c, 2b + d).(2, -3) = 4a + 2c – 6b – 3d

⇒ (2a + c, 2b + d).(2, -3) = 4a – 6b + 2c – 3d

Multiply 2^nd row of matrix Z by matching members of 1^st column of matrix Q, then sum them up.

(3a + 2c, 3b + 2d).(-3, 5) = ((3a + 2c) × -3) + ((3b + 2d) × 5)

⇒ (3a + 2c, 3b + 2d).(-3, 5) = -9a – 6c + 15b + 10d

⇒ (3a + 2c, 3b + 2d).(-3, 5) = -9a + 15b – 6c + 10d

Multiply 2^nd row of matrix Z by matching members of 2^nd column of matrix Q, then sum them up.

(3a + 2c, 3b + 2d).(2, -3) = ((3a + 2c) × 2) + ((3b + 2d) × -3)

⇒ (3a + 2c, 3b + 2d).(2, -3) = 6a + 4c – 9b – 6d

⇒ (3a + 2c, 3b + 2d).(2, -3) = 6a – 9b + 4c – 6d

So, we have

Now, for L.H.S = R.H.S

For matrices having same order, we can write as

-6a + 10b – 3c + 5d = 1 …(i)

4a – 6b + 2c – 3d = 0 …(ii)

-9a + 15b – 6c + 10d = 0 …(iii)

6a – 9b + 4c – 6d = 1 …(iv)

We have 4 variables to find, namely, a, b, c and d; and 4 equations.

So, on adding equations (i) and (iv), we get

(-6a + 10b – 3c + 5d) + (6a – 9b + 4c – 6d) = 1 + 1

⇒ -6a + 6a + 10b – 9b – 3c + 4c + 5d – 6d = 2

⇒ 0 + b + c – d = 2

⇒ d = b + c – 2 …(v)

Now, adding equations (ii) and (iii), we get

(4a – 6b + 2c – 3d) + (-9a + 15b – 6c + 10d) = 0 + 0

⇒ 4a – 9a – 6b + 15b + 2c – 6c – 3d + 10d = 0

⇒ -5a + 9b – 4c + 7d = 0 …(vi)

On adding equations (iv) and (vi), we get

(6a – 9b + 4c – 6d) + (-5a + 9b – 4c + 7d) = 1 + 0

⇒ 6a – 5a – 9b + 9b + 4c – 4c – 6d + 7d = 1

⇒ a + 0 + 0 + d = 1

⇒ d = 1 – a …(vii)

Putting the value of d from equation (vii) in (v), we get

(1 – a) = b + c – 2

⇒ b + c – 2 – 1 = -a

⇒ b + c – 3 = -a

⇒ a = 3 – b – c …(viii)

Now, putting values of a and d from equations (vii) and (viii) in equation (iii), we get

-9(3 – b – c) + 15b – 6c + 10(1 – a) = 0

⇒ -9(3 – b – c) + 15b – 6c + 10(1 – (3 – b – c)) = 0 [∵ a = 3 – b – c]

⇒ -27 + 9b + 9c + 15b – 6c + 10(1 – 3 + b + c) = 0

⇒ -27 + 9b + 9c + 15b – 6c + 10(-2 + b + c) = 0

⇒ -27 + 9b + 9c + 15b – 6c – 20 + 10b + 10c = 0

⇒ 9b + 15b + 10b + 9c – 6c + 10c – 27 – 20 = 0

⇒ 34b + 13c – 47 = 0

⇒ 34b + 13c = 47 …(ix)

Also, putting values of a and d from equations (vii) and (viii) in equation (ii), we get

4(3 – b – c) – 6b + 2c – 3(1 – a) = 0

⇒ 12 – 4b – 4c – 6b + 2c – 3(1 – (3 – b – c)) = 0

⇒ 12 – 4b – 4c – 6b + 2c – 3(1 – 3 + b + c) = 0

⇒ 12 – 4b – 4c – 6b + 2c – 3(-2 + b + c) = 0

⇒ 12 – 4b – 4c – 6b + 2c + 6 – 3b – 3c = 0

⇒ -4b – 6b – 3b – 4c + 2c – 3c + 12 + 6 = 0

⇒ -13b – 5c + 18 = 0

⇒ 13b + 5c = 18 …(x)

On multiplying equation (ix) by 5 and equation (x) by 13, we get

(ix) ⇒ 5(34b + 13c) = 5 × 47

⇒ 170b + 65c = 235 …(xi)

(x) ⇒ 13(13b + 5c) = 13 × 18

⇒ 169b + 65c = 234 …(xii)

Subtracting equations (xi) and (xii), we get

(170b + 65c) – (169b + 65c) = 235 – 234

⇒ 170b – 169b + 65c – 65c = 1

⇒ b = 1

Putting b = 1 in equation (x), we get

13(1) + 5c = 18

⇒ 13 + 5c = 18

⇒ 5c = 18 – 13

⇒ 5c = 5

⇒ c = 1

Putting b = 1 and c = 1 in equation (viii), we get

a = 3 – b – c

⇒ a = 3 – 1 – 1

⇒ a = 3 – 2

⇒ a = 1

Putting a = 1 in equation (vii), we get

d = 1 – a

⇒ d = 1 – 1

⇒ d = 0

Thus, the matrix A is