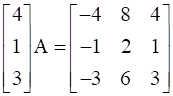We have,

We need to find the matrix A.

Let us see what the order of the matrices given are.

We know what order of matrix is,

If a matrix has M rows and N columns, the order of matrix is M × N.

Order of .

Number of rows = 3

⇒ M = 3

Number of column = 1

⇒ N = 1

Then, order of matrix X = M × N

⇒ Order of matrix X = 3 × 1

Order of .

Number of rows = 3

⇒ M = 3

Number of columns = 3

⇒ N = 3

Then, order of matrix Y = M × N

⇒ Order of matrix Y = 3 × 3

We must understand that, when a matrix of order 1 × 3 is multiplied to the matrix X, only then matrix Y is produced.

Let matrix A be of order 1 × 3, and can be represented as

Then, we get

Take L.H.S:

In order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.

So, we have

Multiply 1^st row of matrix X by matching member of 1^st column of matrix A, then sum them up.

(4)(a) = 4a

Multiply 1^st row of matrix X by matching member of 2^nd column of matrix A, then sum them up.

(4)(b) = 4b

Multiply 1^st row of matrix X by matching member of 3^rd column of matrix A, then sum them up.

(4)(c) = 4c

Multiply 2^nd row of matrix X by matching member of 1^st column of matrix A, then sum them up.

(1)(a) = a

Multiply 2^nd row of matrix X by matching member of 2^nd column of matrix A, then sum them up.

(1)(b) = b

Multiply 2^nd row of matrix X by matching member of 3^rd column of matrix A, then sum them up.

(1)(c) = c

Multiply 3^rd row of matrix X by matching member of 1^st column of matrix A, then sum them up.

(3)(a) = 3a

Multiply 3^rd row of matrix X by matching member of 2^nd column of matrix A, then sum them up.

(3)(b) = 3b

Multiply 3^rd row of matrix X by matching member of 3^rd column of matrix A, then sum them up.

(3)(c) = 3c

Now, L.H.S = R.H.S

Since, the matrices on either sides are of same order, we can say that

4a = -4 …(i)

4b = 8 …(ii)

4c = 4 …(iii)

a = -1 …(iv)

b = 2 …(v)

c = 1 …(vi)

3a = -3 …(vii)

3b = 6 …(viii)

3c = 3 …(ix)

From equation (i), we can find the value of a,

4a = -4

⇒ a = -1

From equation (ii), we can find the value of b,

4b = 8

⇒ b = 2

From equation (iii), we can find the value of c,

4c = 4

⇒ c = 1

And it will satisfy other equations (iv), (v), (vi), (vii), (viii) and (ix) too.

Thus, the matrix A is