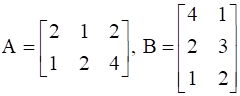
We are given matrices A and B, such that

We are required to find BA and AB, if possible.

Since, in order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.

Let us check for BA.

If a matrix has M rows and N columns, the order of matrix is M × N.

Order of B:

Number of rows = 3

⇒ M = 3

Number of columns = 2

⇒ N = 2

Then, order of matrix B = M × N

⇒ Order of matrix B = 3 × 2

Order of A:

Number of rows = 2

⇒ M = 2

Number of columns = 3

⇒ N = 3

Then, order of matrix A = M × N

⇒ Order of matrix A = 2 × 3

Here,

Number of columns in matrix B = Number of rows in matrix A = 2

So, BA is possible.

Let us check for AB.

Here,

Number of columns in matrix A = Number of rows in matrix B = 3

So, AB is also possible.

Let us find out BA.

Multiply 1^st row of matrix B by matching members of 1^st column of matrix A, then sum them up.

(4, 1).(2, 1) = (4 × 2) + (1 × 1)

⇒ (4, 1).(2, 1) = 8 + 1

⇒ (4, 1).(2, 1) = 9

Multiply 1^st row of matrix B by matching members of 2^nd column of matrix A, then sum them up.

(4, 1).(1, 2) = (4 × 1) + (1 × 2)

⇒ (4, 1).(1, 2) = 4 + 2

⇒ (4, 1).(1, 2) = 6

Similarly, let us calculate in the matrix itself.

Now, let us find out AB.

Multiply 1^st row of matrix A by matching members of 1^st column of matrix B, then sum them up.

(2, 1, 2).(4, 2, 1) = (2 × 4) + (1 × 2) + (2 × 1)

⇒ (2, 1, 2).(4, 2, 1) = 8 + 2 + 2

⇒ (2, 1, 2).(4, 2, 1) = 12

Multiply 1^st row of matrix A by matching members of 2^nd column of matrix B, then sum them up.

(2, 1, 2).(1, 3, 2) = (2 × 1) + (1 × 3) + (2 × 2)

⇒ (2, 1, 2).(1, 3, 2) = 2 + 3 + 4

⇒ (2, 1, 2).(1, 3, 2) = 9

Similarly, let us calculate in the matrix itself.

Thus, and .