If 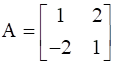 ,
, 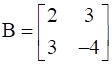 and
and 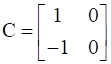 , verify:
, verify:
(i) (AB) C = A (BC)
(ii) A(B + C) = AB + AC
We have matrices A, B and C, such that
![]()
![]()
![]()
In order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.
(i). We need to verify: (AB)C = A(BC)
Take L.H.S = (AB)C
First, compute AB.
![]()
Multiply 1st row of matrix A by matching members of 1st column of matrix B, then sum them up.
(1, 2)(2, 3) = (1 × 2) + (2 × 3)
⇒ (1, 2)(2, 3) = 2 + 6
⇒ (1, 2)(2, 3) = 8
![]()
Multiply 1st row of matrix A by matching members of 2nd column of matrix B, then sum them up.
(1, 2)(3, -4) = (1 × 3) + (2 × -4)
⇒ (1, 2)(3, -4) = 3 – 8
⇒ (1, 2)(3, -4) = -5
![]()
Similarly, let us fill for the rest of elements.
![]()
![]()
![]()
Let ![]() .
.
Now, compute for DC. [∵ (AB)C = DC]
![]()
Multiply 1st row of matrix D by matching members of 1st column of matrix C, then sum them up.
(8, -5)(1, -1) = (8 × 1) + (-5 × -1)
⇒ (8, -5)(1, -1) = 8 + 5
⇒ (8, -5)(1, -1) = 13
![]()
Multiply 1st row of matrix D by matching members of 2nd column of matrix C, then sum them up.
(8, -5)(0, 0) = (8 × 0) + (-5 × 0)
⇒ (8, -5)(0, 0) = 0 + 0
⇒ (8, -5)(0, 0) = 0
![]()
Similarly, let us fill for the rest of elements.
![]()
![]()
![]()
So,
![]()
Take R.H.S: A(BC)
First, compute BC.
![]()
Multiply 1st row of matrix B by matching members of 1st column of matrix C, then sum them up.
(2, 3)(1, -1) = (2 × 1) + (3 × -1)
⇒ (2, 3)(1, -1) = 2 – 3
⇒ (2, 3)(1, -1) = -1
![]()
Multiply 1st row of matrix B by matching members of 2nd column of matrix C, then sum them up.
(2, 3)(0, 0) = (2 × 0) + (3 × 0)
⇒ (2, 3)(0, 0) = 0 + 0
⇒ (2, 3)(0, 0) = 0
![]()
Similarly, let us fill for the rest of the elements.
![]()
![]()
![]()
Let ![]() .
.
Now, compute for AE.
![]()
Multiply 1st row of matrix A by matching members of 1st column of matrix E, then sum them up.
(1, 2)(-1, 7) = (1 × -1) + (2 × 7)
⇒ (1, 2)(-1, 7) = -1 + 14
⇒ (1, 2)(-1, 7) = 13
![]()
Multiply 1st row of matrix A by matching members of 2nd column of matrix E, then sum them up.
(1, 2)(0, 0) = (1 × 0) + (2 × 0)
⇒ (1, 2)(0, 0) = 0 + 0
⇒ (1, 2)(0, 0) = 0
![]()
Similarly, repeat the step for the other elements.
![]()
![]()
![]()
So,
![]()
Thus, (AB)C = A(BC).
(ii). We need to verify: A(B + C) = AB + AC
Take L.H.S: A(B + C)
Add B + C.
![]()
![]()
![]()
Let B + C = F, such that
![]()
Now, multiply A and F.
![]()
Multiply 1st row of matrix A by matching members of 1st column of matrix F, then sum them up.
(1, 2)(3, 2) = (1 × 3) + (2 × 2)
⇒ (1, 2)(3, 2) = 3 + 4
⇒ (1, 2)(3, 2) = 7
![]()
Multiply 1st row of matrix A by matching members of 2nd column of matrix F, then sum them up.
(1, 2)(3, -4) = (1 × 3) + (2 × -4)
⇒ (1, 2)(3, -4) = 3 – 8
⇒ (1, 2)(3, -4) = -5
![]()
Similarly, repeat the steps for the other elements.
![]()
![]()
![]()
So,
![]()
Now, take R.H.S: AB + AC
Compute AB.
![]()
Multiply 1st row of matrix A by matching members of 1st column of matrix B, then sum them up.
(1, 2)(2, 3) = (1 × 2) + (2 × 3)
⇒ (1, 2)(2, 3) = 2 + 6
⇒ (1, 2)(2, 3) = 8
![]()
Multiply 1st row of matrix A by matching members of 2nd column of matrix B, then sum them up.
(1, 2)(3, -4) = (1 × 3) + (2 × -4)
⇒ (1, 2)(3, -4) = 3 – 8
⇒ (1, 2)(3, -4) = -5
![]()
Similarly, repeat the steps for the other elements.
![]()
![]()
![]()
So,
![]()
Now, compute AC.
![]()
Multiply 1st row of matrix A by matching members of 1st column of matrix C, then sum them up.
(1, 2)(1, -1) = (1 × 1) + (2 × -1)
⇒ (1, 2)(1, -1) = 1 – 2
⇒ (1, 2)(1, -1) = -1
![]()
Multiply 1st row of matrix A by matching members of 2nd column of matrix C, then sum them up.
(1, 2)(0, 0) = (1 × 0) + (2 × 0)
⇒ (1, 2)(0, 0) = 0 + 0
⇒ (1, 2)(0, 0) = 0
![]()
Similarly, repeat the steps for the other elements.
![]()
![]()
![]()
So,
![]()
Adding AB + AC.
![]()
Matrices of same order can be added or subtracted.
![]()
![]()
So, clearly L.H.S = R.H.S.
Thus, A(B + C) = AB + AC.