If 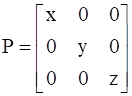 ,
, 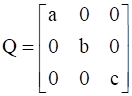 , prove that
, prove that 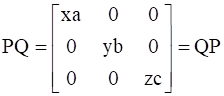
Given: We have matrices P and Q, such that


To Prove: 
Proof: First, we shall compute PQ.

Since, in order to multiply two matrices, A and B, the number of columns in A must equal the number of rows in B. Thus, if A is an m x n matrix and B is an r x s matrix, n = r.
Order of P = 3 × 3
And order of Q = 3 × 3
Number of columns of matrix P = Number of rows of matrix Q = 3
So, P and Q can be multiplied.
So, multiply 1st row of matrix P by matching members of 1st column of matrix Q, then sum them up.
(x, 0, 0)(a, 0, 0) = (x × a) + (0 × 0) + (0 × 0)
⇒ (x, 0, 0)(a, 0, 0) = xa

Multiply 1st row of matrix P by matching members of 2nd column of matrix Q, then sum them up.
(x, 0, 0)(0, b, 0) = (x × 0) + (0 × b) + (0 × 0)
⇒ (x, 0, 0)(0, b, 0) = 0

Similarly, repeat the steps to find other elements.



So,
 …(i)
…(i)
Now, we shall compute QP.

Multiply 1st row of matrix Q by matching members of 1st column of matrix P, then sum them up.
(a, 0, 0)(x, 0, 0) = (a × x) + (0 × 0) + (0 × 0)
⇒ (a, 0, 0)(x, 0, 0) = xa + 0 + 0
⇒ (a, 0, 0)(x, 0, 0) = xa

Similarly, repeat the steps to find other elements.



So,

Thus,  .
.