If ![]() ,
, 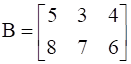 and
and 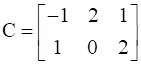 , verify that A(B + C) = (AB + AC).
, verify that A(B + C) = (AB + AC).
We are given the matrices A, B and C, such that
![]()
![]()
![]()
We need to verify that, A(B + C) = AB + AC.
Take L.H.S: A(B + C)
Solving (B + C).
![]()
These matrices can be added as they have same order.
![]()
![]()
Now, multiply A by (B + C).
Let (B + C) = D.
We have,
AD = A(B + C)
![]()
Order of A = 1 × 2
Order of D = 2 × 3
Then, order of resulting matrix = 1 × 3
Multiply 1st row of matrix A by matching members of 1st column of matrix D, then sum them up.
(2, 1)(4, 9) = (2 × 4) + (1 × 9)
⇒ (2, 1)(4, 9) = 8 + 9
⇒ (2, 1)(4, 9) = 17
![]()
Multiply 1st row of matrix A by matching members of 2nd column of matrix D, then sum them up.
(2, 1)(5, 7) = (2 × 5) + (1 × 7)
⇒ (2, 1)(5, 7) = 10 + 7
⇒ (2, 1)(5, 7) = 17
![]()
Multiply 1st row of matrix A by matching members of 3rd column of matrix D, then sum them up.
(2, 1)(5, 8) = (2 × 5) + (1 × 8)
⇒ (2, 1)(5, 8) = 10 + 8
⇒ (2, 1)(5, 8) = 18
![]()
So,
![]()
Now, take R.H.S: AB + AC
Let us compute AB.
![]()
Order of A = 1 × 2
Order of B = 2 × 3
Then, order of AB = 1 × 3
Multiply 1st row of matrix A by matching members of 1st column of matrix B, then sum them up.
(2, 1)(5, 8) = (2 × 5) + (1 × 8)
⇒ (2, 1)(5, 8) = 10 + 8
⇒ (2, 1)(5, 8) = 18
![]()
Similarly, repeat steps to find the rest of the elements.
![]()
![]()
![]()
![]()
Now, let us compute AC.
![]()
Order of AC = 1 × 3
Multiply 1st row of matrix A by matching members of 1st column of matrix C, then sum them up.
(2, 1)(-1, 1) = (2 × -1) + (1 × 1)
⇒ (2, 1)(-1, 1) = -2 + 1
⇒ (2, 1)(-1, 1) = -1
![]()
Similarly, repeat steps to find the rest of the elements.
![]()
![]()
![]()
![]()
Add, AB + AC.
![]()
![]()
![]()
Thus,
A(B + C) = AB + AC.