If 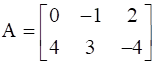 and
and 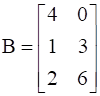 , then verify that:
, then verify that:
(i) (A’)’ = A
(ii) (AB)’ = B’A’
(iii) (kA)’ = (kA’).
We are given with matrices A and B, such that
![]()

(i). We need to verify that, (A’)’ = A.
Take L.H.S: (A’)’
In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal, that is it switches the row and column indices of the matrix by producing another matrix denoted as AT or A’.
So, in transpose of a matrix,
Rows of matrix becomes columns of the same matrix.
So,
If ![]() ,
,
(0, -1, 2) and (4, 3, -4) are 1st and 2nd rows respectively, will become 1st and 2nd columns respectively.
Then 
Also, if  ,
,
Similarly, (0, 4), (-1, 3) and (2, -4) are 1st, 2nd and 3rd rows respectively, will become 1st, 2nd and 3rd columns respectively.
Then ![]()
Note, that ![]()
Thus, verified that (A’)’ = A.
(ii). We need to verify that, (AB)’ = B’A’.
Take L.H.S: (AB)’
Compute AB.

Order of A = 2 × 3
Order of B = 3 × 2
Then, order of AB = 2 × 2
Multiplying 1st row of matrix A by matching members of 1st column of matrix B, then sum them up.
(0, -1, 2)(4, 1, 2) = (0 × 4) + (-1 × 1) + (2 × 2)
⇒ (0, -1, 2)(4, 1, 2) = 0 – 1 + 4
⇒ (0, -1, 2)(4, 1, 2) = 3

Similarly, repeat the process to find the other elements.



![]()
Transpose of AB is (AB)’.
(3, 9) and (11, -15) are 1st and 2nd rows respectively, will become 1st and 2nd columns respectively.
![]()
Take R.H.S: B’A’
If  ,
,
(4, 0), (1, 3) and (2, 6) are 1st, 2nd and 3rd rows of matrix B respectively, will become 1st, 2nd and 3rd columns respectively.
![]()
Also, if ![]() ,
,
(0, -1, 2) and (4, 3, -4) are 1st and 2nd rows respectively, will become 1st and 2nd columns respectively.

Multiply B’ by A’.

Order of B’ = 2 × 3
Order of A’ = 3 × 2
Then, order of B’A’ = 2 × 2
Multiply 1st row of matrix B’ by matching members of 1st column of matrix A’, then sum them up.
(4, 1, 2)(0, -1, 2) = (4 × 0) + (1 × -1) + (2 × 2)
⇒ (4, 1, 2)(0, -1, 2) = 0 – 1 + 4
⇒ (4, 1, 2)(0, -1, 2) = 3

Similarly, repeat the same steps to find out other elements.



![]()
Since, L.H.S = R.H.S.
Thus, (AB)’ = B’A’.
(iii). We need to verify that, (kA)’ = kA’.
Take L.H.S: (kA)’
We know that,
![]()
Multiply k on both sides, (k is a scalar quantity)
![]()
![]()
![]()
Now, to find transpose of kA,
(0, -k, 2k) and (4k, 3k, -4k) are 1st and 2nd rows of matrix kA respectively, will become 1st and 2nd columns respectively.

Take R.H.S: kA’
If ![]()
Then, for transpose of A,
(0, -1, 2) and (4, 3, -4) are 1st and 2nd rows of matrix A respectively, will become 1st and 2nd columns respectively.

Multiply k on both sides,



Note that, L.H.S = R.H.S.
Thus, (kA)’ = kA’.