If 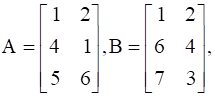 then verify that:
then verify that:
(i) (2A + B)’ = 2A’ + B’
(ii) (A – B)’ = A’ – B’.
We are given matrices A and B, such that


In linear algebra, the transpose of a matrix is an operator which flips a matrix over its diagonal, that is it switches the row and column indices of the matrix by producing another matrix denoted as AT or A’.
So, in transpose of a matrix,
Rows of matrix becomes columns of the same matrix.
(i). We need to verify that, (2A + B)’ = 2A’ + B’.
Take L.H.S: (2A + B)’
Substitute the matrices A and B, in (2A + B)’.





For transpose of (2A + B),
(3, 6), (14, 6) and (17, 15) are 1st, 2nd and 3rd rows respectively, will become 1st, 2nd and 3rd columns respectively.
![]()
Take R.H.S: 2A’ + B’
If  ,
,
(1, 2), (4, 1) and (5, 6) are 1st, 2nd and 3rd rows respectively, will become 1st, 2nd and 3rd columns respectively.
![]()
Multiply both sides by 2,
![]()
![]()
![]()
Also,
If  .
.
(1, 2), (6, 4) and (7, 3) are 1st, 2nd and 3rd rows respectively, will become 1st, 2nd and 3rd columns respectively.
![]()
Now, add 2A’ and B’.
![]()
![]()
![]()
Since, L.H.S = R.H.S
Thus, (2A + B)’ = 2A’ + B’.
(ii). We need to verify that, (A – B)’ = A’ – B’.
Take L.H.S: (A – B)’
Substitute the matrices A and B in (A – B)’.



To find transpose of (A – B),
(0, 0), (-2, -3) and (-2, 3) are 1st, 2nd and 3rd rows respectively, will become 1st, 2nd and 3rd columns respectively.
![]()
Take R.H.S: A’ – B’
If  ,
,
(1, 2), (4, 1) and (5, 6) are 1st, 2nd and 3rd rows respectively, will become 1st, 2nd and 3rd columns respectively.
![]()
Also,
If  ,
,
(1, 2), (6, 4) and (7, 3) are 1st, 2nd and 3rd rows respectively, will become 1st, 2nd and 3rd columns respectively.
![]()
Subtract B’ from A’,
![]()
![]()
![]()
Since, L.H.S = R.H.S
Thus, (A – B)’ = A’ – B’.