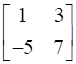
Let A =

To apply elementary row transformations we write:

A = IA where I is the identity matrix

We proceed with operations in such a way that LHS becomes I and the transformations in I give us a new matrix such that

I = XA

And this X is called inverse of A = A^-1

So we have:

Applying R₂→ R₂ + 5R₁

⇒

Applying R₂→ (1/22)R₂

⇒

Applying R₁→ R₁ – 3R₂

⇒

As we got Identity matrix in LHS.

∴ A^-1 =