If 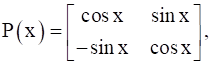 then show that
then show that
P(x).P(y) = P(x + y) = P(y).P(x)
Given,
P(x) = ![]() …(1)
…(1)
P(y) = ![]()
∴ P(x).P(y) = ![]()
⇒ P(x).P(y) = ![]()
We know that-
cos x cos y + sin x sin y = cos (x – y)
cos x sin y + sin x cos y = sin (x + y)
and cos x cos y – sin x sin y = cos (x + y)
⇒ P(x).P(y) = ![]()
In comparison with equation 1 we can say that:
![]() …(2)
…(2)
∴ P(x).P(y) = P(x + y)
Similarly, we can show for P(y).P(x):
P(y).P(x) = ![]()
By matrix multiplication, we have –
P(y).P(x) = ![]()
⇒ P(y).P(x) = ![]()
⇒ P(y).P(x) = ![]() …(3)
…(3)
∴ From equation 2 and 3:
P(x).P(y) = P(y).P(x) = P(x + y) …ans
46