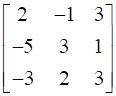
Let A =

To apply elementary row transformations we write:

A = IA where I is the identity matrix

We proceed with operations in such a way that LHS becomes I and the transformations in I give us a new matrix such that

I = XA

And this X is called inverse of A = A^-1

Note: Never apply row and column transformations simultaneously over a matrix.

So we have:

Applying R₂→ R₂ + R₁

⇒ =

Applying R₃→ R₃ - R₂

⇒ =

Applying R₁→ R₁ + R₂

⇒ =

Applying R₂→ R₂ - 3R₁

=

Applying R₃→ (-1)R₃

⇒ =

Applying R₁→ R₁ + 10R₃ and R₂→ R₂ + 17R₃

⇒ =

Applying R₁→ (-1)R₁ and R₂→ (-1)R₂

⇒ =

As we got Identity matrix in LHS.

∴ A^-1 =