Given:

Z=4x + y

From the given figure it is subject to constraints

x + 2y ≥ 4, x +y ≥ 3, x ≥ 0, y ≥ 0

Now let us convert the given inequalities into equation.

We obtain the following equation

x + 2y ≥ 4

⇒ x + 2y = 4

x +y ≥ 3

⇒ x +y = 3

x ≥ 0

⇒ x=0

y ≥ 0

⇒ y=0

The region represented by x + 2y ≥ 4:

The line x + 2y=4 meets the coordinate axes (4,0) and (0,2) respectively. We will join these points to obtain the line x+2y=4. It is clear that (0,0) does not satisfy the inequation x + 2y ≥ 4. So the region that doesn’t contain the origin represents the solution set of the inequation x + 2y ≥ 4

The region represented by x +y ≥ 3:

The line x +y=3 meets the coordinate axes (3,0) and (0,3) respectively. We will join these points to obtain the line x +y=3. It is clear that (0,0) does not satisfy the inequation x +y ≥ 3. So the region that doesn’t contain the origin represents the solution set of the inequation x +y ≥ 3.

Region represented by x≥0 and y≥0 is first quadrant, since every point in the first quadrant satisfies these inequations

The graph of these equations is given.

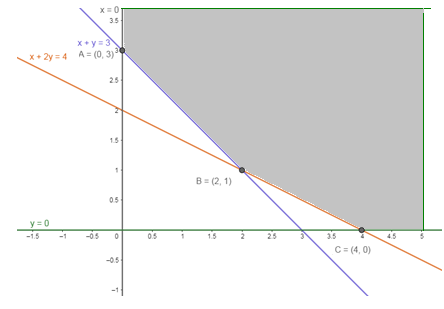
The shaded region ABC is the feasible region is unbounded, and minimum value will occur at a corner point of the feasible region.

Corner Points are A (0, 3), B (2, 1) and C (4, 0)

Now we will substitute these values in Z at each of these corner points, we get

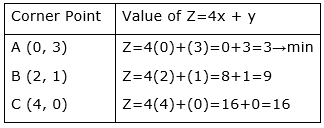
Note that here we see that, the region is unbounded, therefore 3 may not be the minimum value of Z.

To decide this issue, we graph the inequality 4x + y < 3 and check whether the resulting open half plane has no point in common with feasible region otherwise, Z has no minimum value.
From the shown graph above, it is clear that there is no point in common with feasible region and hence Z has minimum value 3 at (0, 3).

Hence, the minimum value of Z is 3 at the point (0, 3).