A company manufactures two types of screws A and B. All the screws have to pass through a threading machine and a slotting machine. A box of Type A screws requires 2 minutes on the threading machine and 3 minutes on the slotting machine. A box of type B screws requires 8 minutes of threading on the threading machine and 2 minutes on the slotting machine. In a week, each machine is available for 60 hours. On selling these screws, the company gets a profit of Rs 100 per box on type A screws and Rs 170 per box on type B screws. Formulate this problem as a LPP given that the objective is to maximise profit.

Question

Philoid · Accepted Answer

Let the company manufactures x boxes of type A screws and y boxes of type B screws. We make the following table from the given data:

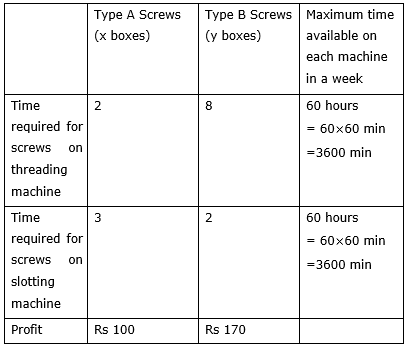
Thus according to the table, the profit becomes, Z=100x+170y

Now, we have to maximize the profit, i.e., maximize Z=100x+170y

The constraints so obtained, i.e., subject to the constraints,

2x+8y≤ 3600 [time constraints for threading machine]

Now will divide throughout by 2, we get

⇒ x+4y≤ 1800…………..(i)

And 3x+2y≤3600 [time constraints for slotting machine]

⇒ 3x+2y≤3600…………..(ii)

And x≥0, y≥0 [non-negative constraint]

So, to maximize profit we have to maximize Z=100x+170y subject to

x+4y≤ 1800

3x+2y≤3600

x≥0, y≥0