Referring exercise 13, we get the following data:

Let the company manufactures x boxes of type A screws and y boxes of type B screws. We make the following table from the given data:

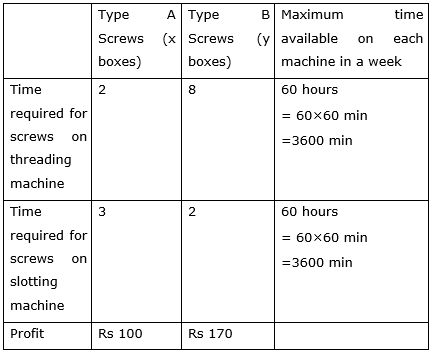
Thus according to the table, the profit becomes, Z=100x+170y

Now, we have to maximize the profit, i.e., maximize Z=100x+170y

The constraints so obtained, i.e., subject to the constraints,

2x+8y≤ 3600 [time constraints for threading machine]

Now will divide throughout by 2, we get

⇒ x+4y≤ 1800…………..(i)

And 3x+2y≤3600 [time constraints for slotting machine]

⇒ 3x+2y≤3600…………..(ii)

And x≥0, y≥0 [non-negative constraint]

So, to maximize profit we have to maximize, Z=100x+170y, subject to

x+4y≤ 1800

3x+2y≤3600

x≥0, y≥0

Now let us convert the given inequalities into equation.

We obtain the following equation

x+4y≤ 1800

⇒ x+4y=1800

3x+2y≤3600

⇒ 3x+2y=3600

x ≥ 0

⇒ x=0

y ≥ 0

⇒ y=0

The region represented by x+4y≤ 1800:

The line x+4y=1800 meets the coordinate axes (1800,0) and (0,450) respectively. We will join these points to obtain the line x+4y=1800. It is clear that (0,0) satisfies the inequation x+4y≤ 1800. So the region that contain the origin represents the solution set of the inequation x+4y≤ 1800

The region represented by 3x+2y≤3600:

The line 3x+2y=3600 meets the coordinate axes (1200,0) and (0,1800) respectively. We will join these points to obtain the line 3x+2y≤3600 . It is clear that (0,0) satisfies the inequation 3x+2y≤3600. So the region that contain the origin represents the solution set of the inequation 3x+2y≤3600

Region represented by x≥0 and y≥0 is first quadrant, since every point in the first quadrant satisfies these inequations

The graph of these equations is given.

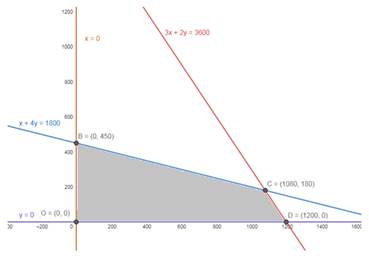
The shaded region OBCD is the feasible region is bounded, and maximum value will occur at a corner point of the feasible region.

Corner Points are O(0, 0), B(0, 450), C(1080, 180) and D(1200, 0)

Now we will substitute these values in Z at each of these corner points, we get

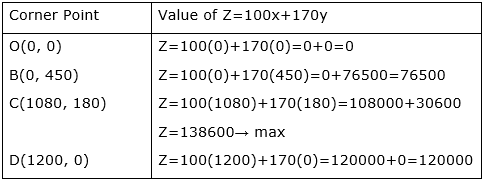
So from the above table the maximum value of Z is at point (1080,180).

Hence, the maximum profit to the manufacturer is Rs. 1,38,600.