Given-

Z = x + y

It is subject to constraints

x + 4y ≤ 8

2x + 3y ≤ 12

3x + y ≤ 9

x ≥ 0, y ≥ 0

We need to maximize Z, subject to the above constraints.

Now let us convert the given inequalities into equation.

We obtain the following equation

x + 4y ≤ 8

⇒ x + 4y = 8

2x + 3y ≤ 12

⇒ 2x + 3y = 12

3x + y ≤ 9

⇒ 3x + y = 9

x ≥ 0

⇒ x=0

y ≥ 0

⇒ y=0

The region represented by x + 4y ≤ 8:

The line x + 4y = 8 meets the coordinate axes (8,0) and (0,2) respectively. We will join these points to obtain the line x + 4y = 8. It is clear that (0,0) satisfies the inequation x + 4y ≤ 8. So, the region containing the origin represents the solution set of the inequation x + y ≤ 8.

The region represented by 2x + 3y ≤ 12:

The line 2x + 3y = 12 meets the coordinate axes (6,0) and (0,4) respectively. We will join these points to obtain the line 2x + 3y = 12. It is clear that (0,0) satisfies the inequation 2x + 3y ≤ 12. So, the region containing the origin represents the solution set of the inequation 2x + 3y ≤ 12

The region represented by 3x + y ≤ 9:

The line 3x + y = 9 meets the coordinate axes (3,0) and (0,9) respectively. We will join these points to obtain the line 3x + y = 9. It is clear that (0,0) satisfies the inequation 3x + y ≤ 9. So, the region containing the origin represents the solution set of the inequation 3x + y ≤ 9

Region represented by x≥0 and y≥0 is first quadrant, since every point in the first quadrant satisfies these inequations.

Plotting these equations graphically, we get

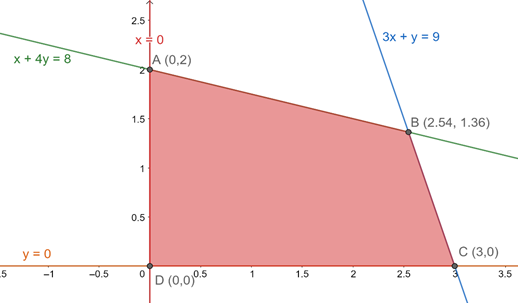
Feasible region is ABCD

Value of Z at corner points A, B, C and D –

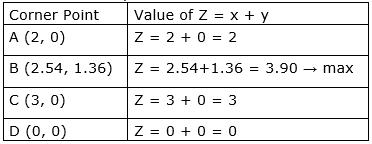
So, value of Z is maximum at B (2.54, 1.36), the maximum value is 3.90.