A manufacturer produces two Models of bikes - Model X and Model Y. Model X takes 6 man-hours to make per unit, while Model Y takes 10 man-hours per unit. There is a total of 450 man-hour available per week. Handling and Marketing costs are Rs 2000 and Rs 1000 per unit for Models X and Y respectively. The total funds available for these purposes are Rs 80,000 per week. Profits per unit for Models X and Y are Rs 1000 and Rs 500, respectively. How many bikes of each model should the manufacturer produce so as to yield a maximum profit? Find the maximum profit.
Let number of bikes per week of model X and Y be x and y respectively.
Given that model X takes 6 man-hours.
So, time taken by x bikes of model X = 6x hours.
Given that model Y takes 10 man-hours.
So, time taken by y bikes of model X = 10y hours.
Total man-hour available per week = 450
So, 6x + 10y ≤ 450
⇒ 3x + 5y ≤ 225
Handling and marketing cost of model X and Y is Rs 2000 and Rs 1000 per unit respectively.
So, total handling and marketing cost of x units of model X and y units of model y is 2000x + 1000y
Maximum amount available for handling and marketing per week is Rs 80000.
So, 2000x + 1000y ≤ 80000
⇒ 2x + y ≤ 80
Profits per unit for Models X and Y are Rs 1000 and Rs 500, Respectively.
Let total profit = Z
So, Z = 1000x + 500y
Also, as units will be positive numbers so x, y ≥ 0
So, we have,
Z = 1000x + 500y
With constraints,
3x + 5y ≤ 225
2x + y ≤ 80
x, y ≥ 0
We need to maximize Z, subject to the given constraints.
Now let us convert the given inequalities into equation.
We obtain the following equation
3x + 5y ≤ 225
⇒ 3x + 5y = 225
2x + y ≤ 80
⇒ 2x + y = 80
x ≥ 0
⇒ x=0
y ≥ 0
⇒ y=0
The region represented by 3x + 5y ≤ 225:
The line 3x + 5y = 225 meets the coordinate axes (75,0) and (0,45) respectively. We will join these points to obtain the line 3x + 5y = 225. It is clear that (0,0) satisfies the inequation 3x + 5y ≤ 225. So, the region containing the origin represents the solution set of the inequation 3x + 5y ≤ 225.
The region represented by 2x + y ≤ 80:
The line 2x + y = 80 meets the coordinate axes (40,0) and (0,80) respectively. We will join these points to obtain the line
2x + y = 80.
It is clear that (0,0) satisfies the inequation 2x + y ≤ 80. So, the region containing the origin represents the solution set of the inequation 2x + y ≤ 80
Region represented by x≥0 and y≥0 is first quadrant, since every point in the first quadrant satisfies these inequations.
Plotting these equations graphically, we get
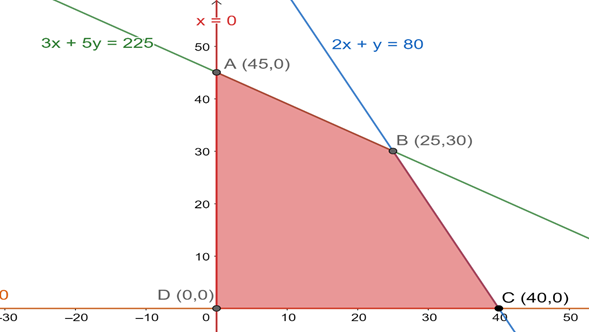
Feasible region is ABCD
Value of Z at corner points A, B, C and D –
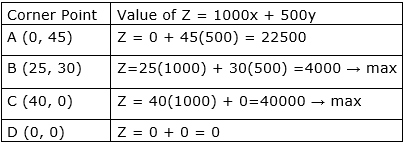
So, value of Z is maximum on-line BC, the maximum value is 40000.So manufacturer must produce 25 number of models X and 30 number of model Y.