A company makes 3 model of calculators: A, B and C at factory I and factory II. The company has orders for at least 6400 calculators of model A, 4000 calculator of model B and 4800 calculator of model C. At factory I, 50 calculators of model A, 50 of model B and 30 of model C are made every day; at factory II, 40 calculators of model A, 20 of model B and 40 of model C are made every day. It costs Rs 12000 and Rs 15000 each day to operate factory I and II, respectively. Find the number of days each factory should operate to minimise the operating costs and still meet the demand.
Let number of days for which factory I operates be x and number of days for which factory II operates be y.
Number of calculators made by factory I and II of model A are 50 and 40 respectively.
Minimum number of calculators of model A required = 6400
So, 50x + 40y ≥ 640
⇒ 5x + 4y ≥ 640
Number of calculators made by factory I and II of model B are 50 and 20 respectively.
Minimum number of calculators of model B required = 4000
So, 50x + 20y ≥ 4000
⇒ 5x + 2y ≥ 400
Number of calculators made by factory I and II of model C are 30 and 40 respectively.
Minimum number of calculators of model C requires = 4800
So, 30x + 40y ≥ 4800
⇒ 3x + 4y ≥ 480
Operating costs is Rs 12000 and Rs 15000 each day to operate factory I and II respectively.
Let Z be total operating cost so we have Z = 12000x + 15000y
Also, number of days are non-negative so, x, y ≥ 0
So, we have,
Constraints,
5x + 4y ≥ 640
5x + 2y ≥ 400
3x + 4y ≥ 480
x, y ≥ 0
Z = 12000x + 15000y
We need to minimize Z, subject to the given constraints.
Now let us convert the given inequalities into equation.
We obtain the following equation
5x + 4y ≥ 640
⇒ 5x + 4y = 640
5x + 2y ≥ 400
⇒ 5x + 2y = 400
3x + 4y ≥ 480
⇒ 3x + 4y = 480
x ≥ 0
⇒ x=0
y ≥ 0
⇒ y=0
The region represented by 5x + 4y ≥ 640:
The line 5x + 4y = 640 meets the coordinate axes (128,0)
and (0,160) respectively. We will join these points to obtain the line 5x + 4y = 640. It is clear that (0,0) does not satisfy the inequation 5x + 4y ≥ 640. So, the region not containing the origin represents the solution set of the inequation 5x + 4y ≥ 640.
The region represented by 5x + 2y ≥ 400:
The line 5x + 2y = 400 meets the coordinate axes (80,0) and (0,200) respectively. We will join these points to obtain the line x + y = 7. It is clear that (0,0) does not satisfy the inequation 5x + 2y ≥ 400. So, the region not containing the origin represents the solution set of the inequation 5x + 2y ≥ 400.
The region represented by 3x + 4y ≥ 480:
The line 3x + 4y = 480 meets the coordinate axes (160,0) and (0,120) respectively. We will join these points to obtain the line 3x + 4y = 480. It is clear that (0,0) does not satisfy the inequation 3x + 4y ≥ 480. So, the region not containing the origin represents the solution set of the inequation 3x + 4y ≥ 480.
Region represented by x≥0 and y≥0 is first quadrant, since every point in the first quadrant satisfies these inequations.
Plotting these equations graphically, we get
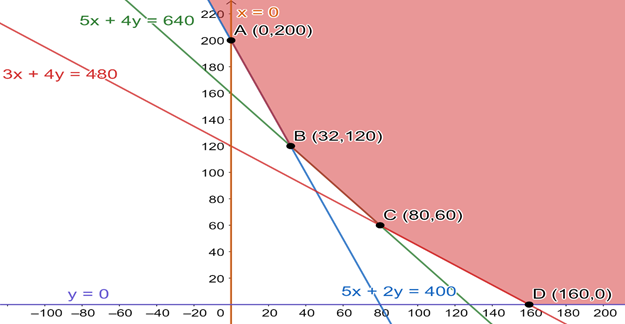
Feasible region is the region to the right of ABCD
Feasible region is unbounded.
Value of Z at corner points A, B, C and D –
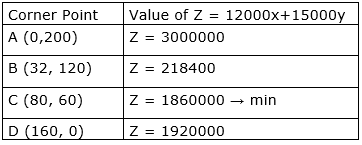
Now, we plot 12000x + 15000y<1860000, to check if resulting open half has any point common with feasible region.
The region represented by 12000x + 15000y<1860000:
The line 12000x + 15000y=1860000 meets the coordinate axes (155,0) and (0,124) respectively. We will join these points to obtain the line 12000x + 15000y=1860000. It is clear that (0,0) satisfies the inequation 12000x + 15000y<1860000. So, the region containing the origin represents the solution set of the inequation 12000x + 15000y<1860000.
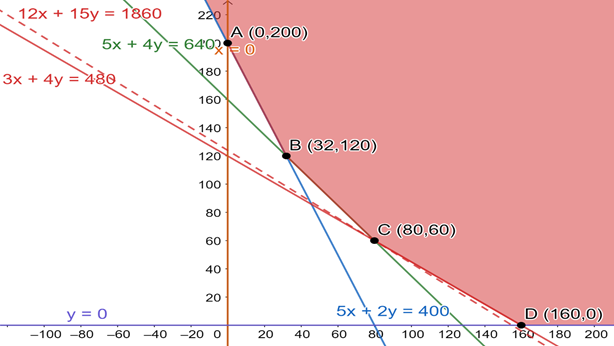
Clearly, 12000x + 15000y<1860000 intersects feasible region only at C.
So, value of Z is minimum at C (80, 60), the minimum value is 1860000.
So, number of days factory I is required to operate is 80 and number of days factory II should operate is 60 to minimize the cost.