Find the value of k so that the function f is continuous at the indicated point: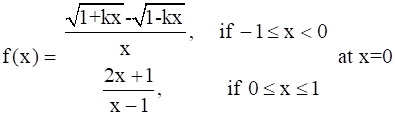
Given,
 …(1)
…(1)
We need to find the value of k such that f(x) is continuous at x = 0.
A function f(x) is said to be continuous at x = c if,
Left hand limit(LHL at x = c) = Right hand limit(RHL at x = c) = f(c).
Mathematically we can represent it as-
![]()
Where h is a very small number very close to 0 (h→0)
Now, let’s assume that f(x) is continuous at x = 0.
∴ ![]()
As we have to find k so pick out a combination so that we get k in our equation.
In this question we take LHL = f(0)
∴ ![]()
⇒ ![]() {using eqn 1}
{using eqn 1}
⇒ ![]() -1
-1
As we can’t find the limit directly because it is taking 0/0 form.
So, we will rationalize it.
⇒ ![]() -1
-1
Using (a+b)(a-b) = a2 – b2 , we have –
 -1
-1
⇒ ![]() -1
-1
⇒ ![]() -1
-1
⇒ ![]() = -1
= -1
∴ 2k/2 = -1
∴ k = -1
13