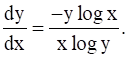
x = e^cos2t and y = e^sin2t

Now x = e^cos2t,

Taking log on both sides to get,

log x = cos 2t

For y = e^sin2t

Taking log on both sides we get,

log y = sin 2t

∴ cos²2t + sin²2t = (log x)² + (log y)²

1 = (log x)² + (log y)²

Differentiating w.r.t x,