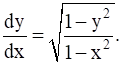
Given:

Put x = sin α and y = sin β …(i)

Now, we know that sin²θ + cos² θ = 1

⇒ cos α + cos β = a( sin α – sin β) …(ii)

Now, we use some trigonometry formulas,

So, eq.(ii) become

⇒ 2 cot^-1 a = α – β …(iii)

Now, from eq.(i), we have

α = sin^-1 x and β = sin^-1 y

Now, put value of α and β in eq. (iii), we get

2 cot^-1 a = sin^-1 x – sin^-1 y

or sin^-1 x – sin^-1 y = 2cot^-1 a

On differentiating above with respect to x, we get

Hence Proved