Given: f(x) = log (x² + 2) – log3

Now, we have to show that f(x) verify the Rolle’s Theorem

First of all, Conditions of Rolle’s theorem are:

a) f(x) is continuous at (a,b)

b) f(x) is derivable at (a,b)

c) f(a) = f(b)

If all three conditions are satisfied then there exist some ‘c’ in (a,b) such that f’(c) = 0

Condition 1:

f(x) = log (x² + 2) – log3

Since, f(x) is a logarithmic function and logarithmic function is continuous for all values of x.

⇒ f(x) = log (x² + 2) – log3 is continuous at x ∈ [-1,1]

Hence, condition 1 is satisfied.

Condition 2:

f(x) = log (x² + 2) – log3

On differentiating above with respect to x, we get

⇒ f(x) is differentiable at [-1,1]

Hence, condition 2 is satisfied.

Condition 3:

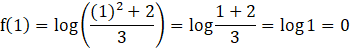
∴f(-1) = f(1)

Hence, condition 3 is also satisfied.

Now, let us show that c ∈ (-1,1) such that f’(c) = 0

Put x = c in above equation, we get

∵, all the three conditions of Rolle’s theorem are satisfied

f’(c) = 0

⇒ 2c = 0

⇒ c = 0 ∈ (-1, 1)

Thus, Rolle’s theorem is verified.