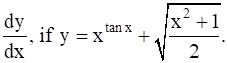
_{We have,}

Putting x^tanx = u and

u = x^tanx

_{Taking log on both sides, we get}

_{log u = tanx log x}

_{Differentiating w.r.t x, we get}

_⇒

_⇒

_⇒ (i)

Now,

⇒

_{Differentiating w.r.t x, we get}

_⇒

_⇒ (ii)

Now, y = u + v

⇒

On substituting the values of from (i) and (ii),we get

_⇒

_⇒