The set of points where the function f given by f(x) = |2x – 1| sinx differentiable is

Question

Philoid · Accepted Answer

We have, f(x) = |2x – 1| sinx

Now, 2x-1 = 0

⇒

Now we will check the differentiability of f(x) at 1/2.

=

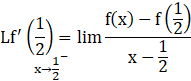
= (∵ f(x) = |2x – 1| sinx)

=

= (∵ f(x) = |2x – 1| sinx)

=

∴

Hence, f(x) is not differentiable at