If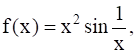 
where 
, then the value of the function f at x = 0, so that the function is continuous at x = 0, is
We have, 
where x ≠ 0.
Given that, the function is continuous at x = 0
⇒ 
⇒ 
⇒ f(0) = 0 × (an oscillating number between -1 and 1 )
⇒ f(0) = 0
Hence,the value of the function f at x = 0 is ‘0’.
88