For the function 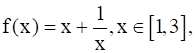the value of c for mean value theorem is

Question

Philoid · Accepted Answer

Mean Value Theorem states that, Let f : [a, b] → R be a continuous function on [a, b] and differentiable on (a, b). Then there exists some c in (a, b) such that

We have,

Since, f(x) is a polynomial function it is continuous on [1,3] and differentiable on (1,3).

Now, as per Mean value Theorem, there exists at least one c ∈ (1,3), such that

⇒

⇒ 3(c² – 1) = 2c²

⇒ 3c² – 2c² = 3

⇒ c² = 3

⇒