(i)

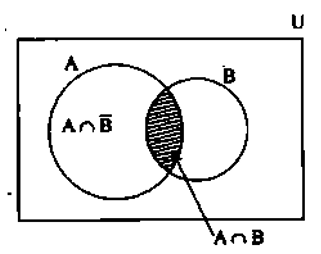
WE HAVE TO PROVE,

P(A)= P(AՈB) + P(AՈ)

We know A = AՈS

We can write s = A Ս A^’ and s = B Ս B^’

So,

A = A Ո (B Ս B^’)

= (A Ո B) Ս (A Ո B^’)

Two events are mutually exclusive or disjoint if they cannot both occur at the same time.

(A Ո B) means A and B both occurring at the same time while (A Ո B^’) means A and B^’ both occurring at the same time.

So, it is not possible that (A Ո B) and (A Ո B^’) occur at the same time.

Hence (A Ո B) and (A Ո B^’) are mutually exclusive.

When events are mutually exclusive then P (A Ո B) = 0

∴ P[(A Ո B) Ո (A Ո B^’)] = 0 ….. (1)

So, A = A Ո (B Ս B^’)

As we know P (A Ս B) = P (A) + P(B) - P (A Ո B)

P(A) = P [(A Ո B) Ս (A Ո B^’)]

= P (A Ո B) + P (A Ո B^’) – P [(A Ո B) Ո (A Ո B^’)]

From (1),

P(A) = P(AՈB) + P(AՈ)

Hence proved

(ii)WE HAVE TO PROVE, P(AՍB) = P(AՈB) + P(AՈ) + P(ՈB)

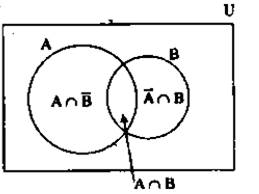
AՍB means the all the possible outcomes of both A and B.

From the Venn diagram we can see,

AՍB = (AՈB) Ս (AՈ) Ս (ՈB)

Two events are mutually exclusive or disjoint if they cannot both occur at the same time.

(A Ո B) means A and B both occurring at the same time while (A Ո B^’) means A and B^’ both occurring at the same time.

(ՈB) means A^’ and B both occurring at the same time.

So, it is not possible that (A Ո B), (A Ո B^’) and (ՈB) occur at the same time.

Hence (A Ո B), (A Ո B^’) and (ՈB) are mutually exclusive.

When events are mutually exclusive then P (A Ո B) = 0

P [(A Ո B) Ո (A Ո B^’)] =0 ….. (1)

P [(A Ո B^’) Ո P(ՈB)] = 0 ….. (2)

P [(A Ո B) Ո P(ՈB)] = 0 ….. (3)

P [(A Ո B) Ո (A Ո B^’) Ո P(ՈB)] = 0 …. (4)

P(AՍB) = P[(AՈB) Ս (AՈ) Ս (ՈB)]

We know,

P(A ∪ B ∪ C) = P(A) + P(B) + P(C) − P(A ∩ B) − P(A ∩ C) − P(B ∩ C) + P(A ∩ B ∩ C)

So,

P(AՍB) = P[(AՈB) Ս (AՈ) Ս (ՈB)] = P(AՈB) + P(AՈ) + P(ՈB) – P[(AՈB) ∩ (AՈ] – P[(AՈB) ∩ (ՈB)]− P[(AՈ) ∩ (ՈB)] + P [(A Ո B) Ո (A Ո B^’) Ո P(ՈB)]

From (1), (2), (3) and(4) we get,

P(AՍB) = P(AՈB) + P(AՈ) + P(ՈB)

Hence proved.