Two probability distributions of the discrete random variable X and Y are given below.

Question

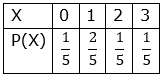
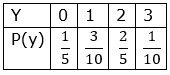
Two probability distributions of the discrete random variable X and Y are given below. Prove that E(Y) 2 =2E(X).

Philoid · Accepted Answer

Since, we have to prove that, E(Y²) =2E(X) -----(i)

Taking LHS of equation (i), we have:

E(Y)²= Y²P(Y)

=

……(ii)

Now taking RHS of equation (i) we get:

E(X)= XP(X)

……..(iii)

Thus, from equations (ii) and (iii), we get:

E(Y²) =2E(X)

Hence proved.