Refer to Question 41 above. If a white ball is selected, what is the probability that it came from
(i) Bag 2 (ii) Bag 3
Referring to the previous solution, using Bayes theorem, we have
Let E1, E2, and E3 be the events that Bag 1, Bag 2 and Bag 3 is selected, and a ball is chosen from it.
Bag 1: 3 red balls,
Bag 2: 2 red balls and 1 white ball
Bag 3: 3 white balls.
As The probability that bag i will be chosen and a ball is selected from it is i|6.
![]()
Let F be the event that a white ball is selected.
So, P(F|E1) is the probability that white ball is chosen from the bag 1.
P(F|E2) is the probability that white ball is chosen from the bag 2.
P(F|E3) is the probability that white ball is chosen from the bag 2.
P(F|E1) = 0
![]()
![]()
We have to find the probability that if white ball is selected it is selected from:
(i) Bag 2
We use Bayes’ theorem to find the probability of occurrence of an event A when event B has already occurred.
![]()
P(E2|F) is the probability that white ball is selected from bag 2.
![]()
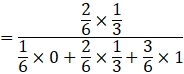
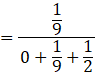
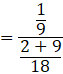
![]()
![]()
(ii)Bag 3
We use Bayes’ theorem to find the probability of occurrence of an event A when event B has already occurred.
![]()
P(E3|F) is the probability that white ball is selected from bag 2.
Using Bayes’ theorem, we get the probability of P(E3|F) as:
![]()
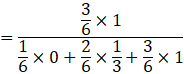
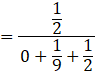
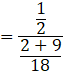
![]()
![]()