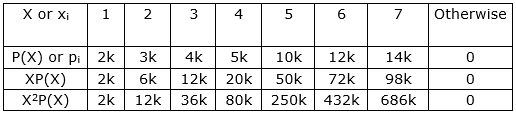
Let X be a discrete random variable whose probability distribution is defined as follows:
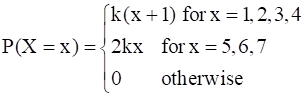
where k is a constant. Calculate
(i) the value of k (ii) E (X) (iii) Standard deviation of X.
Given:
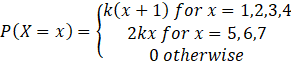
Thus, we have the probability distribution of X is

(i) the value of k
We know that,
Sum of the probabilities = 1
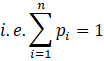
∴ 2k + 3k + 4k + 5k + 10k + 12k + 14k = 1
⇒ 50k = 1
![]()
⇒ k = 0.02
(ii) To find: E(X)
The probability distribution of X is:

Therefore,
μ = E(X)
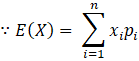
∴ E(X) = 2k + 6k + 12k + 20k + 50k + 72k + 98k + 0
= 260k
![]()
![]()
= 5.2 …(i)
(iii) To find: Standard deviation of X
We know that,
Var(X) = E(X2) – [E(X)]2
= ΣX2P(X) – [Σ{XP(X)}]2
= [2k + 12k + 36k + 80k + 250k + 432k + 686k +0] – [5.2]2 = 1498k – 27.04
![]()
= 29.96 – 27.04
= 2.92
We know that,
standard deviation of X = √Var(X) = √2.92 = 1.7088
≅ 1.7