The probability distribution of a random variable x is given as under:
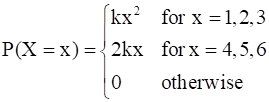
where k is a constant. Calculate
(i) E(X) (ii) E (3X2) (iii) P(X ≥ 4)
Given:

We know that,
Sum of the probabilities = 1
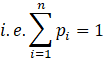
⇒ k + 4k + 9k + 8k + 10k + 12k = 1
⇒ 44k = 1
![]()
(i) To find: E(X)
We know that, μ = E(X)
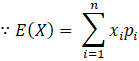
or
E(X) = ΣXP(X)
= 1 × k + 2 × 4k + 3 × 9k + 4 × 8k + 5 × 10k + 6 × 12k
= k + 8k + 27k + 32k + 50k + 72k
= 190k
![]()
![]()
= 4.32
(ii) To find: E(3X2)
Firstly, we find E(X2)
We know that,
E(X2) = ΣX2P(X)
= 12 × k + 22 × 4k + 32 × 9k + 42 × 8k + 52 × 10k + 62 × 12k
= k + 16k + 81k + 128k + 250k + 432k
= 908k
![]()
= 20.636
≅ 20.64
∴ E(3X2) = 3 × 20.64 = 61.92
(iii) P(X ≥ 4) = P(X = 4) + P(X = 5) + P(X = 6)
= 8k + 10k + 12k
= 30k
![]()
![]()
51