If P(A) = 2|5, P(B) = 3|10 and P(A ∩ B) = 1|5, the P(A′|B′).P(B′|A′) is equal to

Question

Philoid · Accepted Answer

We have,

P(A’|B’) × P(B’) = P(A’ ∩ B’)

…(i)

P(B’|A’) × P(A’) = P(B’ ∩ A’)

…(ii)

On multiplying eq. (i) and (ii), we get

[∵P(A’ ∩ B’) = P[(A ∪ B)’]= 1 – P(A ∪ B)]

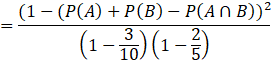
[Additive law of Probability]

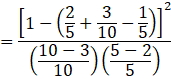
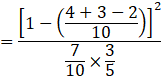
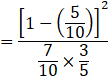
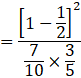
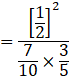
Hence, the correct option is C