Let E denotes the event that student ‘A’ solves the problem correctly.

∴ P(E) = 1/3

Similarly, if we denote the event of ’B’ solving the problem correctly with F

We can write that:

P(F) = 1/4

Note: Observe that both the events are independent.

∴ Probability that both the students solve the question correctly can be represented as-

P (E ∩ F) = = P(E₁) {say} {we can multiply because events are independent}

∴ Probability that both the students could not solve the question correctly can be represented as-

P(E’ ∩ F’) = = P(E₂) {say}

Now we are given with some more data and they can be interpreted as:

Given: probability of making a common error and both getting same answer.

Note: If they are making an error, we can be sure that answer coming out is wrong.

Let S denote the event of getting same answer.

∴ above situation can be represented using conditional probability.

P(S|E₂) = 1/20

And if their answer is correct obviously, they will get same answer.

∴ P(S|E₁) = 1

We need to find the probability of getting a correct answer if they committed a common error and got the same answer.

Mathematically,

i.e P(E₁|S) = ?

By observing our requirement and availability of equations, we can make guess that Bayes theorem is going to help us.

∴ Using Bayes theorem, we get-

P(E₁|S) =

Using the values from above –

P(E₁|S) =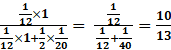

Clearly our answer matches with option D.

∴ Option (D) is the only correct choice.